I've had a discussion with a few people within Princeton as to the lessons that can be learned from what only can be called a debacle. In particular I think there are two major errors in these structure determinations with the second one being the more pernicious of the two. The discussion on the CCP4 news group seemed to focus on the first of these errors: the accidental inversion of the sign of the anomalous signal in the multiwavelength anomalous dispersion (MAD) structure determination. As I'll show later, the inversion of this sign inevitably leads to an inversion of the electron density map. This error, while not insignificant, is catchable and is intrinsically related to the sort of ambiguity that is present in Multiple Isomorphous Replacement (MIR) structure determinations. An inverted structure would contain left-handed α-helices and D-amino acids, so cannot be easily built using the conventional right-handed helices and L-amino acids. The second error, therefore, is the forcing of a structure with conventional geometry into a density map consistent only with inverted geometry.
In the News secton of that weeks' Science, Greg Miller discussed the ramifications of the retraction (Miller (2006) Science 314:1856-1857). A few things came to light: first is that Chang's postdoc advisor Doug Rees and Chang's departmental head Peter Wright have been quoted in a supportive manner. The second is that in a quote within Miller's News article, the author of the Sev1866 study and ex-colleague of Chang's was somewhat less charitable:
Interpreting the "hand" of a molecule is always a challenge for crystallographers, Locher notes, and many mistakes can lead to an incorrect mirror-image structure. Getting the wrong hand is "in the category of monumental blunders", Locher says.
For what it's worth, I tend to agree more with Locher's assessement. To err is human. To err in the literature five times smacks of something closer to carelessness.
Jones and Kleywegt subsequently published a letter in Science entitled "Experimental Data for Structure Papers" (see Science 13 July 2007: Vol. 317. no. 5835, pp. 194 - 195) in which this case was cited as a renewed plea for the requirement of deposition of experimental data (i.e. structure factors, experimental phases). Brian Matthews also published a comment in Protein Science covering many of the same aspects as this page - see B.W.Matthews Protein Science (2007), 16:1013-1016. Greg Petsko also has a commentary on it: "And the second shall be first" at Genome Biology (Genome Biology 2007, 8:103). There are quite a few other commentaries as well, since this event spawned much discussion, but I'm not going to attempt to be comprehensive.
An in-house data reduction program introduced a change in sign for the anomalous differences. This program, which was not part of a conventional data processing package, converted the anomalous pairs (I+ and I-) to (F- and F+), thereby introducing a sign change.The first thing to note is that SCALEPACK goes out of its way to avoid you being able to switch the sign of I+ and I- during scaling, and that DENZO always integrates the data with the correct hand (although tinkering with Yscale would allow you to get this wrong). Using the well-debugged CCP4 package you're unlikely to encounter random bugs in the suite that flip the sign of the anomalous difference. That's the advantage of using widely-used software vs your own programs - raelly pernicious bugs have been uncovered by other lucky souls.
When you collect, process and scale data using DENZO and SCALEPACK the output .sca file contains a set of averaged intensities I(hkl). If you output the data with the ANOMALOUS or SCALE ANOMALOUS flags then SCALEPACK puts I(h,k,l) and I(-h,-k,-l) on one line. The shorthand frequently used for these values are I+ and I-, respectively. If you use a program like SCALEPACK2MTZ, then this data gets imported into CCP4's MTZ format with little change. If you then use TRUNCATE, the I+ and I- values (intensities) are converted to structure factor moduli (|F|) values (basically by square-rooting the intensities). The output could be expressed as |F+| and |F-| but is just as frequently converted to F and Δano where Δano is the difference between |F+| and |F-| and F is the mean of |F+| and |F-|. This data gets used by programs like SHARP or PHENIX to find the heavy atom substructure and used for phasing. Programs like SHELX use the original SCALEPACK .sca file but essentially work in the same way. If in subsequent steps I leave off the moduli signs remember that structure factors from experimental data are without phases so we only know the magnitude (|F|) of the structure factor, and lack knowledge of the phase of F.
If you inadvertently change the sign on the anomalous signal, you essentially centrosymmetrically invert the dataset. Since Δano is (|F+|-|F-|) it follows that -Δano is (|F-|-|F+|) so implicitly F+ becomes F- and vice versa. One has misassigned (h,k,l) to (-h,-k,-l) and vice versa. Using this inverted dataset for an MIR calculation would make no difference whatsoever because |F+| = |F-| by Friedel's Law. However using this inverted dataset for a MAD calculation means that what you'd consider to be the "correct" solution will be one that is centrosymmetrically inverted with respect to the true correct solution. To see why this is, consider the structure factor equation:
F(hkl) = Σatoms f(S)e-BS2/4e2πi(hx+ky+lz)
f(S) is the atomic scattering factor where S is the diffraction vector, exp(-BS2/4) is the B-factor correction (thermal motion) and the final exponential term is one that relates the offset due to atom location and the Miller indices. You can see that location (x,y,z) with Miller index (h,k,l) produces exactly the same structure factor as (-x,-y,-z) with (-h,-k,-l) i.e. both amplitude and phase. I.E. if you invert the structure factors centrosymmetrically you essentially invert the structure centrosymmetrically. The usage of "S" in this equation denotes the magnitude of S (S=h.a* + k.b* + l.c*) which is the same for (h,k,l) and (-h,-k,-l).
Note that this is not the same thing as Friedel's Law:
|F(hkl)| = |F(-h-k-l)| and &phi(hkl) = -&phi(hkl)
because Friedel's Law requires that the phase is inverted when (hkl) is inverted. However both the amplitude and phase are the same in the (hkl)/(xyz) (-h-k-l)/(-x-y-z) pairs.Friedel's Law is the reason why we cannot distinguish the hand of an MIR solution simply from phasing or solvent-flatting statistics alone. Since we must determine heavy atom locations from magnitudes alone, there is an inherent ambiguity between a set of heavy atom positions (x,y,z) and those at the inverted location (-x,-y,-z). We cannot distinguish between those simply by inspection of a Patterson map - this is a Fourier calculated with |F(hkl)|2 coefficients and all phases zero - because the Patterson map itself is centrosymmetric as a consequence of discarding the phases. When it comes time to phase from these atoms by MIR, there's also no way from statistics alone to distinguish the correct hand case from the inverted case because |F(hkl)| = |F(-h-k-l)| for non-anomalous data and so the statistics of the correct hand map and the inverted map are identical. Therefore one distinguishes hand by inspection of the electron density map and applying one's prior structural knowledge about protein features.
In the MAD case we also cannot distinguish between heavy atom sites (x,y,z) and (-x,-y,-z) because we have no phases at the point when we are searching for them. However the anomalous component of diffraction does not obey Friedel's Law so an SIRAS, MIRAS, MAD map should have different statistics during solvent flattening depending on whether you have the correct or incorrect hand. Generally speaking if your phases are good enough to produce an interpretable map, they are good enough to provide a clear distinction between the correct and incorrect hands.
However if you have inverted the index of the dataset via inverting the sign of the anomalous signal you've put yourself into a situation where what appears to be the correct hand is one that is in reality an inverted copy of the map. Everything (phases, sites, structure factors, indexing) at this point is self-consistent and so looks statistically "correct" but with a centrosymmetrically inverted map.
Since I've solved quite a few MAD structures in the Shi lab this situation is fairly easy to simulate. For this example I'm using the SeMet data collected at BNL's X25 beamline for the MC159 crystal structure (Li, Jeffrey, Wu and Shi (2006) J.Biol.Chem 281:2960). Space group P212121 a=35.10 b=63.50 c=76.46. I take a regular set of .sca files containing anomalous signal and also construct another set of equivalent .sca files but with I+ and I- exchanged courtesy of a program I wrote for this purpose. If we run my standard set of SHELX scripts on these sets of .sca files we find the following:
Conventional data..... SHELXC: Correlation coefficients (%) between signed anomalous differences Resl. Inf - 8.0 - 6.0 - 5.0 - 4.0 - 3.5 - 3.0 - 2.6 - 2.4 - 2.2 - 2.0 - 1.75 LREM/HREM 69.3 74.9 58.5 34.9 -2.0 26.1 23.9 22.0 22.2 18.3 17.0 LREM/PEAK 50.1 65.6 49.3 32.5 2.6 26.0 22.3 16.6 25.6 25.5 20.1 LREM/INFL 63.7 70.0 53.5 39.5 2.1 26.8 24.4 19.2 22.6 26.8 22.4 HREM/PEAK 93.4 95.4 92.3 75.7 67.1 63.7 68.2 65.5 60.9 59.2 57.0 HREM/INFL 95.2 94.2 91.2 81.0 77.3 68.3 71.8 69.4 64.8 65.0 61.1 PEAK/INFL 96.6 96.0 96.9 86.3 78.7 78.9 81.8 79.2 74.7 71.1 67.3 SHELXD: (output and .res file) Try 50, CC All/Weak 41.82 / 30.15, best 42.03 / 30.45, best PATFOM 13.70 SE01 1 .813812 .447632 .061134 1.0000 0.2 SE02 1 .644669 .537468 -.012909 .9821 0.2 SE03 1 1.082550 .543900 -.094383 .8218 0.2 SE04 1 1.381027 .542450 -.213280 .6300 0.2 (additional weak sites deleted) SHELXE: non-inverted sites, 35% solvent, 100 cycles wt = .300, Contrast = .309, Connect. = .889 for dens.mod. cycle 100 SHELXE: inverted sites, 35% solvent, 100 cycles wt = .300, Contrast = .473, Connect. = .912 for dens.mod. cycle 100clearly in this case compared to the solution found by SHELXD the best map is with the coordinates inverted. Expecting the coordinates to be inverted is a reflection that the phasing method is unable to distinguish the correct absolute hand of the heavy atom locations, rather than anything to do with the sign of the anomalous signal.
Inverted data...... SHELXC: Correlation coefficients (%) between signed anomalous differences Resl. Inf - 8.0 - 6.0 - 5.0 - 4.0 - 3.5 - 3.0 - 2.6 - 2.4 - 2.2 - 2.0 - 1.75 LREM/HREM 69.3 74.9 58.5 34.9 -2.0 26.1 23.9 22.0 22.2 18.3 17.0 LREM/PEAK 50.1 65.6 49.3 32.5 2.6 26.0 22.3 16.6 25.6 25.5 20.1 LREM/INFL 63.7 70.0 53.5 39.5 2.1 26.8 24.4 19.2 22.6 26.8 22.4 HREM/PEAK 93.4 95.4 92.3 75.7 67.1 63.7 68.2 65.5 60.9 59.2 57.0 HREM/INFL 95.2 94.2 91.2 81.0 77.3 68.3 71.8 69.4 64.8 65.0 61.1 PEAK/INFL 96.6 96.0 96.9 86.3 78.7 78.9 81.8 79.2 74.7 71.1 67.3 SHELXD: (output and .res file) Try 50, CC All/Weak 40.49 / 28.51, best 40.64 / 28.74, best PATFOM 13.13 SE01 1 .315712 .551605 .061517 1.0000 0.2 SE02 1 .144417 .463516 -.012260 .9653 0.2 SE03 1 .582588 .456276 -.094505 .8167 0.2 SE04 1 .882179 .454437 -.213257 .6442 0.2 SHELXE: non-inverted sites, 35% solvent, 100 cycles wt = .300, Contrast = .305, Connect. = .875 for dens.mod. cycle 100 SHELXE: inverted sites, 35% solvent, 100 cycles wt = .300, Contrast = .477, Connect. = .913 for dens.mod. cycle 100Note that the heavy atom locations in the second case are related to the first ones by the transformation (x+1/2,-y,z) - this matrix has a determinant of -1 although the actual transformation is (-x,-y,-z) combined with a symmetry operator (-x,1/2+y,1/2-z) and a (0,1/2,1/2) relative origin shift (see the description of alternative origins in CCP4).
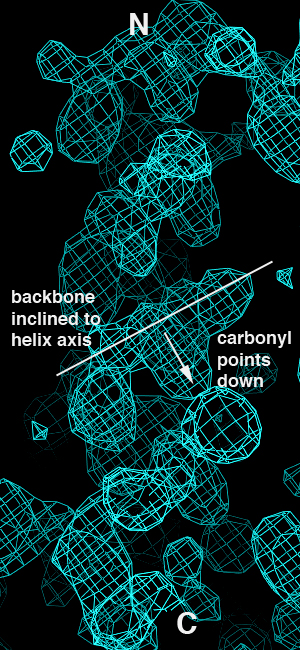
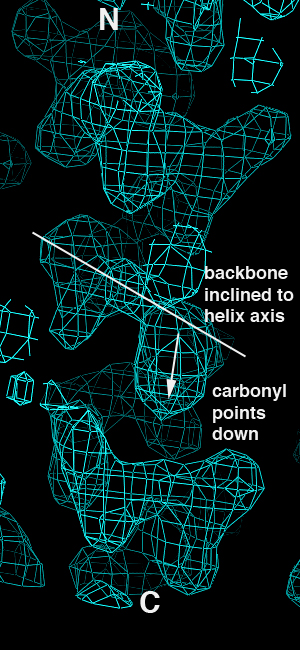
This isn't a shock - we should get essentially the same results from the correct and inverted datasets since they still contain the same magnitudes but differ only in terms of the anomalous sign. When we look at the maps, however, we immediately see that the inverted hand gives rise to inverted helical electron density:
| Correct Hand | Inverted Hand |
|---|---|
 |
 |
The problem is that having made the first error, the structure was built into the inverted map and refined without anyone noticing that the density was telling them that the map was inverted. This is a class of error I call "forcing", and is the snafu I think of as being the most pernicious one in this particular case. Note that a total of five papers on two different structures were published, so there was considerable opportunity to catch the error. Such an opportunity was not apparently taken advantage of.
Part of the complication here is limited resolution, and this was compounded by the authors' willingness to use less conventional refinement techniques to force the R-factor and R-free down into the "publishable range". The original 2001 paper reporting MsbA was only at 4.5Å resolution, determined my MAD from an Osmium derivative. The R-factor and R-free for a conventional single copy of the model as 38% and 45% respectively. The use of multicopy refinement, in which multiple non-interacting copies of the molecule are used to model disorder, increased the number of parameters in the model considerably (16 copies) and reduced the R-free to 38%. It has been hypothesized on the CCP4 newsgroup that part of the thing that got the R-free down as far as it did (and 38% is pretty high, but there are plenty of structures whose R-free stuck in the low 30's) is the random selection of R-free flags allowed mixing of the R-free and R-work sets by virtue of the 8-fold non-crystallographic symmetry. What is interesting is that Fig 3c of that paper appears to show experimental density that shows a decent amount of helical definition (presumably averaged, but the figure legend does not specify) which should have allowed the inverted nature of the helices to be discovered.
The MsbA paper from May 2005 with vanadate and lipopolysaccharide was determined by 5.5Å mercury SAD, so again the experimental phases allowed independent verification of the structure, and again the same set of mistakes were made. The native was at 4.2Å, with only 2-fold non-crystallographic symmetry. Apart from citing R-factor and R-free no details of the crystallographic refinement were given - one wonders if this was a multicopy refinement also, or if somehow they managed to get their R-free down to 33% at 4.2Å resolution with conventional methods.
The EmrE paper from later in 2005 was apparently determined by Arsenate MAD and SeMet SAD at 4.0Å and 6.0Å respectively. The refinement is quoted as R-factor of 28% and R-free of 35% at a resolution of 4.0Å but again details of the refinement are minimal.
What appears to have happened is an excess of enthusiasm in the lab in question in hammering on an incorrect interpretation of the structure until it was in the "publication range" for refinement statistics. To do this once is bad enough, but not unprecedented. To do this multiple times in succession over multiple years and to not catch the error borders on the inexcusible.
The lesson to be learnt, I hope, from all this is that one must approach one's interpretation of a structure with appropriate skepticism and conservatism and to always be open to the possibility of error. This ABC transporter story is one of the more notable debacles in structural biology in recent memory.
Phil Jeffrey, Jan 2007, expressing his own opinions.
(updated in minor ways various times since).